RL-Theory

强化学习2:MDP Reinforcement Learning2 Markov Decision Process

概述

本文基于 DeepMind RL Research 领头人David Silver的Intro to RL教学视频和互联网上各大神的笔记统一整理，如有错误请斧正，谢谢！

为了一步步引入MDP，我们将循序渐进地从马尔科夫性质（Markov Process），马尔科夫奖励过程（Markov Reward Process，MRP），再到马尔科夫决策过程（Markov Decision Processes,MDP）。最后再对MDP进行部分扩展，如有限与连续MDPs(Infinite and continuous MDPs)，部分观测MDP（Partially Observable MDPs，POMDP）以及无折扣或平均奖励MDPs(Undiscounted, average reward MDPs)。

1. 马尔科夫性质（Markov Property）

进一步了解马尔科夫决策过程之前，需要先了解马尔科夫性质(Markov Property)，马尔科夫性质即未来的状态只依赖于当前状态，与过去状态无关。
正式的定义如下：

马尔科夫性质（Markov Property）定义：
在时间步时，环境的反馈仅取决于上一时间步的状态，与时间步以及步之前的时间步都没有关联性。

马尔科夫性，也就是无后效性。根据定义，当前状态捕捉了历史中所有相关的信息，所以知道了状态，状态是未来的充分统计。某阶段的状态一旦确定，则此后过程的演变不再受此前各状态及决策的影响，历史 (history) 就可以完全丢弃。也就是说，未来与过去无关。举个不恰当的例子：A股某些医疗股的变化指数。。。

然而在实际的环境中，智能体所需完成的任务不能够完全满足马尔科夫性质，即在时间步的反馈不一定仅仅依赖于时间步的状态和动作。但是为了简化问题的求解过程，仍然假设该任务满足马尔科夫属性（Markov Property），并通过约束环境的状态使得问题满足马尔科夫属性。

2. 马尔科夫过程（Markov Process）

Probability of outcome of state � depends on the state of the previous �
outcomes.

AKA Markov Chain. 是一个无记忆的随机过程，可有用元组表示，其中为有限数量的状态集，为状态转移概率矩阵。

为有限的状态空间集，表示时间步的状态，其中。

为状态转移矩阵，

状态与状态之间的转换过程即为马尔科夫过程。虽然我们可能不知道P的具体值到底是什么，但是通常我们假设P是存在的（转移概率存在，如果是确定的，无非就是概率为1），而且是稳定的（意思是从状态A到其他状态的转移虽然符合某个分布，但是其转移到某个状态的概率是确定的，不随时间变化的）。

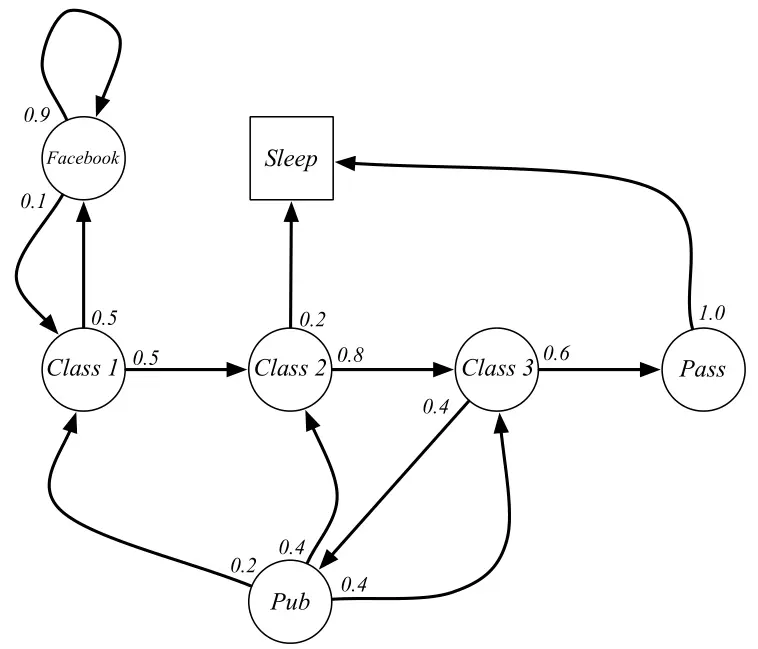
上图中，圆圈表示学生所处的状态，方格Sleep是一个终止状态，终止状态也可以理解成以100%的概率转移到自己，所以一旦进入，就停留在此。箭头表示状态之间的转移，箭头上的数字表示状态转移概率。

例如，当学生处在第一节课（Class1）时，有50%的概率会上第2节课（Class2）；同时也有50%的概率不认真听课，进入到刷facebook这个状态中。在刷facebook这个状态时，比较容易沉迷，有90%的概率在下一时刻继续浏览，有10%的概率返回到第一节课。当学生进入到第二节课（Class2）时，会有80%的概率继续参加第三节课（Class3），有20%的概率觉得课程较难而被迫下课（Sleep）。当学生处于第三节课这个状态时，有60%的概率通过考试，继而100%的结课，也有40%的概率去泡吧。泡吧之后，又分别有20%、40%、40%的概率返回值第一、二、三节课重新继续学习。

假设学生马尔科夫链从状态Class1开始，最终结束于Sleep。其间的过程根据状态转化图可以有很多种可能性，这些都称为采样片段Sample Episodes。以下四个Episodes都是可能的：

C1 - C2 - C3 - Pass - Sleep

C1 - FB - FB - C1 - C2 - Sleep

C1 - C2 - C3 - Pub - C2 - C3 - Pass - Sleep

C1 - FB - FB - C1 - C2 - C3 - Pub - C1 - FB - FB - FB - C1 - C2 - C3 - Pub - C2 - Sleep

2.1 马尔科夫链与Episode

Episode可以翻译为片段、情节、回合等，在强化学习问题中，一个Episode就是一个马尔科夫链，根据状态转移矩阵可以得到许多不同的episode，也就是多个马尔科夫链。

强化学习问题分两种：

如果一个任务总能达到终态，结束任务或者开启下一轮任务，那么这个任务就被称为回合任务，也就是episode任务。例如，让一个智能体学习如何下围棋，围棋棋盘只有那么大，游戏定会终局，所以是一个回合式任务。
如果一个任务可以无限持续下去，永远不会结束，即永远在训练当中，那么这个任务就被称为连续性任务。例如，教会一辆车能够进行自动驾驶就是一个连续性任务，不要钻牛角尖说能源会耗尽，车子会磨损，我们只聚焦问题与环境本身，不涉及其他非稳定因素。

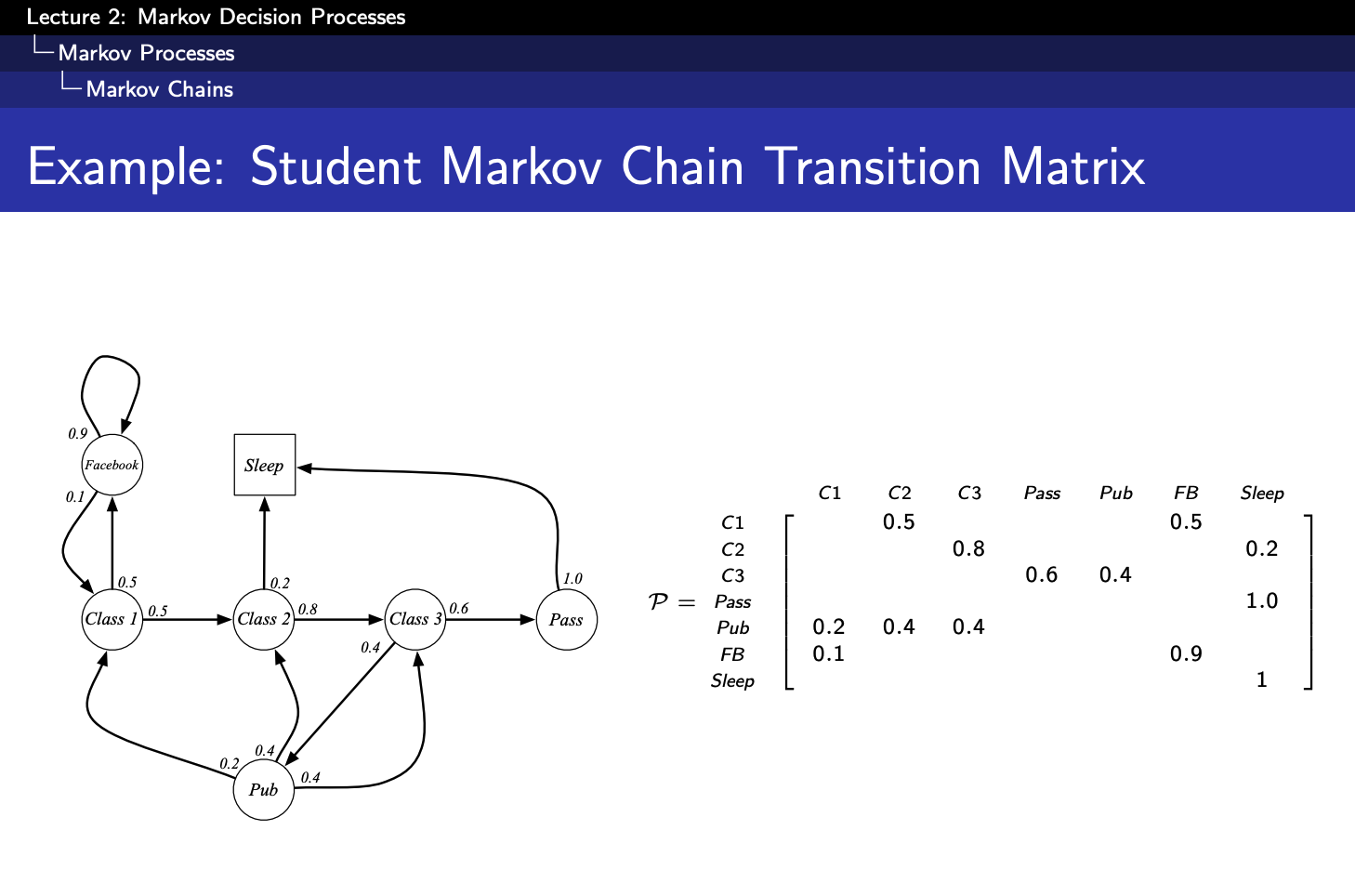
3. 状态转移矩阵(State Transition Matrix)

对于马尔科夫状态以及后续的状态，状态转移概率可以定义为：。状态转移矩阵是马尔科夫过程中状态之间转移的概率所组成的矩阵，因此大小是状态数的平方。它反映了所有当前状态以及后续的状态的映射，所以它的每行概率之和必定为 1。

Markdown版本：

4.马尔科夫奖励过程(Markov Reward Process)

原本的马尔科夫过程加上奖励值R之后就变成了马尔科夫奖励过程，元素由变为。其中R就是奖励，是折扣因子。

马尔科夫奖励过程(Markov Reward Process)定义：

一个马尔科夫奖励过程(MRP)，由一个四元组构成：

S为有限的状态空间集，表示时间步的状态，其中。

为状态转移矩阵，

R为奖励函数，

为折扣因子，

为了找到长期累积奖励，不仅要考虑当前时间步t的奖励，还需要考虑到未来的奖励。总奖励（Total Reward）的计算公式如下：

根据总奖励R的计算公式可知，长期累积奖励从当前时间步开始，直到最终状态的奖励，得到未来累积奖励(Future Cumulative Reward)。

一般而言，环境是随机的或者未知的，这意味着下一个状态可能也是随机的。即由于所处的环境是随机的，所以无法确定下一次执行相同的动作，以及是否能够获得相同的奖励。向未来探索得越多，可能产生的分歧(不确定性)就越多。因此，在实际任务中，通常用折扣未来累积奖励（Discounted Future Cumulative Reward）来代替未来累积奖励。

如果考虑到无限时间的场景，更加通用的表示为（当前获得的奖励表示为）：

其中为折扣因子（Discount Factor），是介于的常数。对于距离当前时间步越远的奖励，其重要性就越低。

当γ=0时,状态S的值完全由其转移的期望立即奖励表示,即一点都不关心未来，可以认为该策略“目光短浅”。
当γ=1时,状态S的值由以当前状态为始态,运行至终态所得到的所有立即奖励加和的值表示,即未来与现在同等重要，看起来就像非常“有远见“。
当0<γ<1时,状态S的值是前两个模式的trade-off,即对未来看重的程度由γ决定。倘若想平衡当前时间的奖励与未来的奖励，可设置为一个较大的值，比如。如果环境是恒定的，或者说环境的所有状态是已知（Model-based）,那么未来累积奖励可以提前获得并不需要进行折扣计算，这时候可以简单的将折扣因子设置为1。

4.2 回报（Return）与折扣因子

大多数的马尔科夫奖励过程（MRP）与马尔科夫决策过程（MDP）都会使用折扣因子。主要基于如下几点考虑：

数学上计算的便利性。在带环的马尔可夫过程中，可以避免陷入无限循环来的无限大回报，达到收敛。
随着时间的推移，，未来的不确定性越来越大
类比经济学中，眼前的利益比未来的利益更加有意义
人类的行为也更加倾向于眼前利益
退一步来说，令为1，也可以简单的转化成没有折扣因子的状态

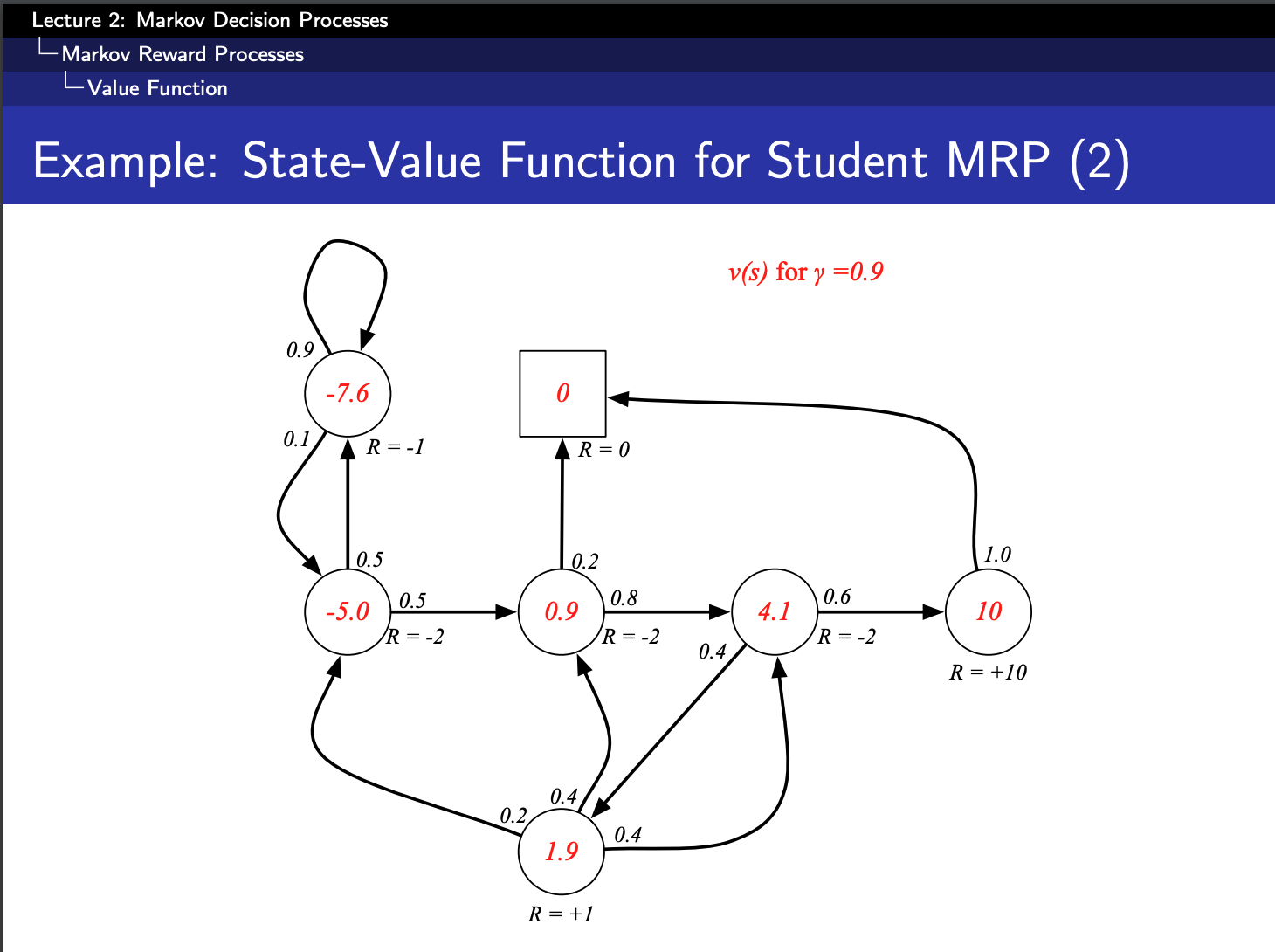
4.3. 价值函数(Value Function)

价值函数是状态的长期价值表示。它是上面说的回报的期望。

在概率论和统计学中，数学期望是试验中每次可能的结果的概率乘以结果值得总和。这里回报的期望，即价值函数会会随着折扣因子的变化而取不同的值，因为回报会因为的值而改变，期望自然也就会改变。

上图是为0.9时，例子中的马尔科夫奖励过程，红色的就是状态的价值。

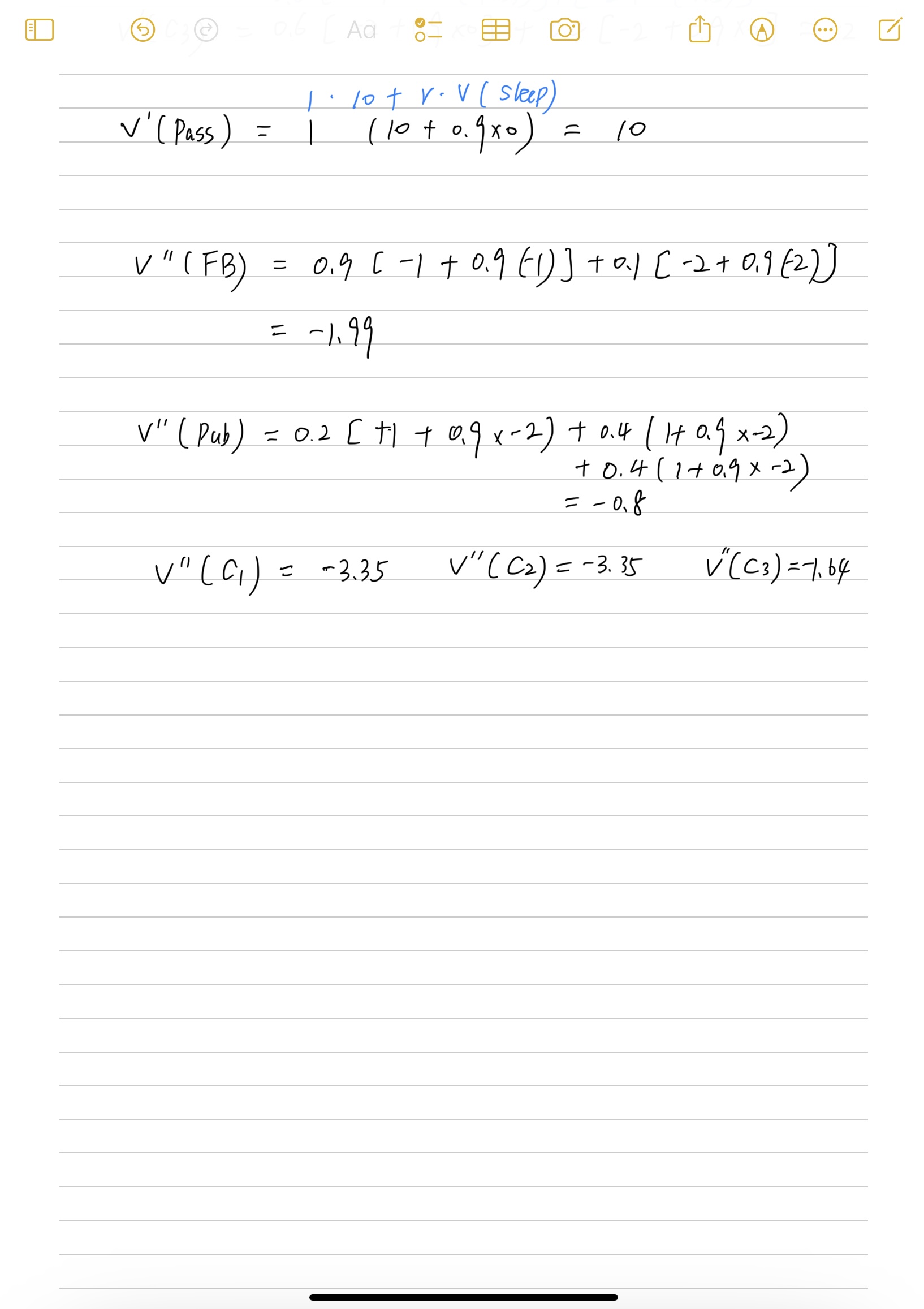
通过价值函数的公式我们可以知道,要想求解一个状态的状态价值，需要根据马尔科夫链把所有的可能列出来。每个可能都在终点终止，但是上面这个马尔科夫过程其实是有环的，可能陷入无限循环的局面。

因为折扣因子还是1，所以会导致回报G无限大，期望也就无限大，状态价值V也就无限大。下一章节引入贝尔曼方程就是为了更好的求解价值函数的。

以下是python代码：

//initialization
V_fb = 0;
V_pub =0;
V_c1 = 0;
V_c2 = 0;
V_c3 = 0;
V_pass = 0;
V_slp = 0;
gamma =0.9;

//Iteratively computing Value function
for n in  range(1,30):
    V_fb_next  = 0.9*(-1+gamma*V_fb) + 0.1*(-1+gamma*V_c1)
    V_pub_next = 0.2*(1+gamma*V_c1) + 0.4*(1+gamma*V_c2)+0.4*(1+gamma*V_c3)
    V_c1_next  = 0.5*(-2+gamma*V_c2) + 0.5*(-2+gamma*V_fb)
    V_c2_next  = 0.2*(-2+gamma*V_slp) + 0.8*(-2+gamma*V_c3)
    V_c3_next  = 0.6*(-2+gamma*V_pass) + 0.4*(-2+gamma*V_pub)
    v_pass_next = 1*(10 + 0.9*V_slp)

    V_fb = V_fb_next;
    V_pub = V_pub_next;
    V_c1 = V_c1_next;
    V_c2 = V_c2_next;
    V_c3 = V_c3_next;
    v_pass =v_pass_next

print("fb = ",V_fb);
print("pub=",V_pub);
print("V_c1 =",V_c1)
print("V_c2 =",V_c2)
print("V_c3 =",V_c3)

About this Post

This post is written by Rui Xu, licensed under CC BY-NC 4.0.

#AI #Reinforcement Learning