Using the Minimax Algorithm to implement the Basic Human-Machine Confrontation Game
本文介绍了编写一个名为“奥赛罗”的Java程序来玩反转棋游戏。
Reversi是在一个8 * 8的棋盘上玩的双人棋游戏♟。棋子分为黑白两色,故称“黑白棋”;因为行棋之时将对方棋子翻转,变为己方棋子,故又称“翻转棋”(Reversi)。
游戏规则
在下面的描述中,线段的定义是形成连续直线(水平、垂直或对角线)的一系列棋盘方块。
玩家放置棋子的规则是该棋子必须放置在一个空的方块上,使得有一条线段穿过所下的棋子,然后穿过一个或多个相反颜色的棋子,并以玩家自己颜色的棋子结束。
当存在这样一条线段时,我们说对手在该线段上的棋子被包围起来。
游戏规定黑棋先走。
当放置一个棋子时,被包围的棋子会根据以下规则改变颜色:
- 对于每一条线段穿过所玩的棋子,然后穿过一个或多个相反颜色的棋子,并以玩家自己颜色的棋子结束,则该线段所穿过的相反颜色的棋子全部更改为玩家自己的颜色棋子。
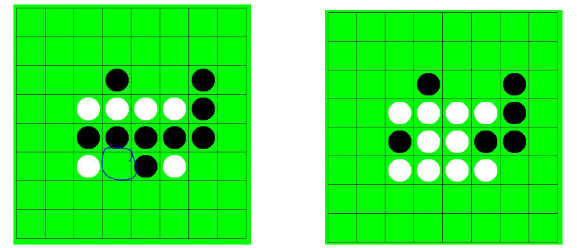
在本图中,左图显示了白方可能采取的走法,将对手的三个棋子括起来,形成右图所示的位置。 |
当且仅当一名玩家无法移动而其对手可以移动时,该玩家就错过了一个回合。 当两个玩家都无法移动时游戏结束。(这种情况通常(但并非总是)发生,因为所有方格都已被占据。)获胜者是棋盘上自己颜色的棋子数量较多的玩家; 如果没有这样的玩家,则结果为平局。
类文件,配置具体介绍
玩家端(人类)
- 主要的游戏逻辑是在 BoardState 中。
- 数字代表颜色(1表示白色;-1表示黑色,0代表没有)
- getContents(int x, int y) 和 void setContents(int x, int y, int piece) 允许在棋盘方块上检索和设置。
- boolean checkLegalMove(int x, int y), 它检查当前玩家是否有可能在正方形(x,y)上移动。
- 检索当前玩家的合法移动列表的方法是ArrayList
getLegalMoves()。此方法返回当前玩家的所有合法移动。
机器端(电脑)
计算机端(电脑)位于MoveChooser.java 中,其中的
main程序创建了一个实例。这个类所做的唯一的事情是实现静态方法
chooseMove(BoardState boardState)在它的当前版本中,这个方法只是获取合法的移动,如果该列表为空,则返回null(记住我说的有时会没有合法的移动),否则返回该列表中的第一个移动。在这里我们写一个更好的移动选择函数,而不是每次仅默认选择第一个。我们使用minimax with αβ-pruning 方法来优化。
- 首先赋予棋盘每个位置相应的权重,为后续通过计算路线成本来规划最佳路线做准备。
> 这些数字反映了一个玩家在各自的方块上的价值。请注意,边缘上的正方形具有很高的值(因为这里的块很难取),而角落上的正方形具有更高的值(因为这里不能取块)。相比之下,相邻的方块有负值,因为这里的一块将允许对手移动到一个高值的方块上。然后,板位置的值可以通过将白块占据的所有方块的权重加起来,然后减去黑块占据的所有方块的权重来定义。
1
2
3
4
5
6
7
8
9
10
11// numbers reflect the value for a player of being on the respective square
public static int positionValue[][] = {
{120, -20, 20, 5, 5, 20, -20, 120},
{-20, -40, -5, -5, -5, -5, -40, -20},
{20, -5, 15, 3, 3, 15, -5, 20},
{5, -5, 3, 3, 3, 3, -5, 5},
{5, -5, 3, 3, 3, 3, -5, 5},
{20, -5, 15, 3, 3, 15, -5, 20},
{-20, -40, -5, -5, -5, -5, -40, -20},
{120, -20, 20, 5, 5, 20, -20, 120},
};接下来是常规初始化:返回一个包含合法移动的列表,是否有合法移动可用。
1
2
3
4
5
6
7public static Move chooseMove(BoardState boardState){
ArrayList<Move> moves = boardState.getLegalMoves();
if(moves.isEmpty()){
return null;
}
return topLevel(boardState, moves);
}下面是游戏🎮的分值计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17///////////////////////////////////////////////// write a better move selection function ///////////////////////////////////////
// board position = + weights of all those squares occupied by white pieces - weights of those squares occupied by black pieces.
public static int staticEvaluation(BoardState boardState){
int weight = 0;
for(int i=0; i<8; i++){
for(int j=0; j<8; j++){
// white
if(boardState.getContents(i, j)== 1){
weight += positionValue[i][j];
// black
}else if(boardState.getContents(i,j)== -1){
weight -= positionValue[i][j];
}
}
}
return weight;
}使用MiniMax算法进行游戏博弈的静态方法。它接受一个BoardState对象作为游戏状态,一个搜索深度searchDepth,以及alpha、beta和maximizingNode作为MiniMax算法的参数,并返回一个整数值。
首先,代码获取当前游戏状态下的合法移动,存储在move列表中。
接下来,代码根据不同的条件进行分支处理:
如果searchDepth为0,即达到了搜索的最大深度,代码将调用staticEvaluation(boardState)方法对当前游戏状态进行静态评估,并返回评估值。
如果maximizingNode为真,表示当前节点为最大化节点(轮到最大化玩家走子),代码将执行Max节点的逻辑。
如果以上条件都不满足,表示当前节点为最小化节点(轮到最小化玩家走子),代码将执行Min节点的逻辑。Max节点的逻辑:
将alpha初始化为最小整数值,表示下界。
对于每个合法移动,进行以下操作:- 如果alpha >= beta,即上界小于等于下界,或者move列表为空,退出循环。
- 创建一个boardState对象的深拷贝,用于模拟在当前移动下的新游戏状态。
- 对深拷贝的boardState对象调用makeLegalMove(move.get(i).x, move.get(i).y)方法,执行当前移动。
- 调用miniMax(boardState1, searchDepth-1, alpha, beta, false)方法,以递归方式搜索下一层的最小化节点,并将返回值存储在miniVal中。
如果miniVal大于alpha,更新alpha的值为miniVal。
返回alpha作为当前节点的评估值。
Min节点的逻辑:
将beta初始化为最大整数值,表示上界。
对于每个合法移动,进行以下操作:- 如果alpha >= beta,即上界小于等于下界,或者move列表为空,退出循环。
- 创建一个boardState对象的深拷贝,用于模拟在当前移动下的新游戏状态。
- 对深拷贝的boardState对象调用makeLegalMove(move.get(i).x, move.get(i).y)方法,执行当前移动。
- 调用miniMax(boardState1, searchDepth-1, alpha, beta, true)方法,以递归方式搜索下一层的最大化节点,并将返回值存储在maxVal中。
如果maxVal小于beta,更新beta的值为maxVal。
返回beta作为当前节点的评估值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39// αβ-pruning DFS
public static int miniMax(BoardState boardState, int searchDepth, int alpha, int beta, Boolean maxmizingNode){
ArrayList<Move> move = boardState.getLegalMoves();
if(searchDept == 0){
return staticEvaluation(boardState);
}else if(maxmizingNode){
alpha = Integer.MIN_VALUE; // lower bound
for(int i = 0 ; i<move.size(); i++){
if(alpha >= beta || move.isEmpty()){
break;
}
// a fresh copy of boardState
BoardState boardState1 = boardState.deepCopy();
boardState1.makeLegalMove(move.get(i).x, move.get(i).y);
int miniVal = miniMax(boardState1, searchDepth-1, alpha, beta, false); // next is minimizing
if(alpha < miniVal){ // update alpha
alpha = miniVal;
}
}
return alpha;
}else{
beta = Integer.MAX_VALUE; // upper bound
for(int i = 0; i<move.size(); i++){
if(alpha >= beta||move.isEmpty()){
break;
}
// a fresh copy of boardState
BoardState boardState1 = boardState.deepCopy();
boardState1.makeLegalMove(move.get(i).x, move.get(i).y);
int maxVal = miniMax(boardState1, searchDepth-1, alpha, beta, true); // next is maxmizing
if(maxVal < beta){ // update beta
beta = maxVal;
}
}
return beta;
}
}顶层调用与后续调用略有不同,因为您必须选择产生最佳子节点的着法(从计算机玩家的角度来看),而不是简单地评估子节点的值。 重要的是,当且仅当没有可用的移动时,程序才返回空移动。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23// The top-level call
public static Move topLevel(BoardState bs, ArrayList<Move> move){
// searchDepth 设置成8保证运行速度和智能程度的权衡
int searchDepth= Othello.searchDepth;
int valueIndex = 0;
int a = Integer.MIN_VALUE; // negative infinity
int b = Integer.MAX_VALUE; // positive infinity
Move bestChoice = null; // set when there are no moves available as the default value
for(int i=0; i<move.size(); i++){
BoardState temp = bs.deepCopy();
temp.makeLegalMove(move.get(i).x, move.get(i).y);
int minimax = miniMax(temp, searchDepth-1, a, b, false); // at the beginning set to minimizing node
if(a<minimax){
a=minimax;
valueIndex = i;
}
}
bestChoice = move.get(valueIndex);
return bestChoice;
}
}- 首先赋予棋盘每个位置相应的权重,为后续通过计算路线成本来规划最佳路线做准备。
游戏运行注意事项
- 当且仅当一个玩家不能移动,但TA的对手可以移动时,TA才算错过这个回合。
- 人类玩家(总是黑色)与计算机(总是白色)颜色保持不变。
- 点击不合法动作的方块会产生警告声;如果轮到玩家(人类)下棋,但玩家没有合法的移动 ,那么玩家必须点击棋盘上的任何地方以允许游戏传递到电脑;
- 如果玩家想玩另一个游戏,需要关闭窗口,重新运行程序。
- 最好在电脑“思考”时不要点击以进行干扰。
- 最后,作为一种特别的刺激,如果游戏以电脑的移动而结束,那么玩家必须点击棋盘才能看到结果。
About this Post
This post is written by Rui Xu, licensed under CC BY-NC 4.0.